Elektronikindo.com – Pengertian dan Hukum Aljabar Boolean. Aljabar Boolean adalah cabang matematika yang mendasarkan operasinya pada logika boolean, yang merupakan sistem logika yang hanya memiliki dua nilai atau keadaan yang mungkin: benar (true) dan salah (false).
Aljabar Boolean memiliki aplikasi luas dalam ilmu komputer, teknik elektronika, dan bidang-bidang lain yang melibatkan manipulasi data digital. Dalam aljabar Boolean, terdapat berbagai hukum yang membentuk dasar-dasar operasionalnya. Mari kita bahas lebih lanjut tentang pengertian aljabar Boolean dan beberapa hukum yang relevan.
Pengertian Aljabar Boolean
Aljabar Boolean dinamai setelah George Boole, seorang matematikawan Inggris abad ke-19. Konsep utama di balik aljabar Boolean adalah penggunaan operasi logika pada variabel boolean, yang hanya dapat memiliki nilai benar (true) atau salah (false).
Dalam konteks ini, variabel boolean menggambarkan keadaan suatu entitas, seperti saklar elektronik yang dapat berada dalam keadaan “nyala” (true) atau “mati” (false).
Operasi dasar dalam aljabar Boolean meliputi AND, OR, dan NOT. Operasi ini mirip dengan operasi logika dalam bahasa sehari-hari.
Misalnya, operasi AND menghasilkan nilai benar hanya jika kedua variabel yang terlibat adalah benar, sementara operasi OR menghasilkan nilai benar jika salah satu atau keduanya adalah benar.
Hukum Aljabar Boolean
Ada beberapa hukum dasar dalam aljabar Boolean yang membentuk dasar-dasar operasionalnya. Beberapa hukum ini mencakup:
1. Hukum Identitas
– AND: A AND 1 = A
– OR : A OR 0 = A
2. Hukum Nihil
– AND: A AND 0 = 0
– OR : A OR 1 = 1
3. Hukum Dominasi
– AND: A AND A’ = 0
– OR : A OR A’ = 1
4. Hukum Komplemen
– AND: A AND A’ = 0
– OR : A OR A’ = 1
5. Hukum Distribusi
– AND over OR: A AND (B OR C) = (A AND B) OR (A AND C)
– OR over AND: A OR (B AND C) = (A OR B) AND (A OR C)
6. Hukum De Morgan
– De Morgan’s AND: (A AND B)’ = A’ OR B’
– De Morgan’s OR : (A OR B)’ = A’ AND B’
Hukum-hukum ini membantu dalam menyederhanakan ekspresi boolean, membuat analisis dan manipulasi lebih efisien.
Aplikasi Aljabar Boolean
Aplikasi Aljabar Boolean sangat luas dan mendalam, terutama dalam dunia teknologi informasi, komputer, dan rekayasa elektronika. Di bawah ini adalah beberapa contoh penting dari aplikasi Aljabar Boolean:
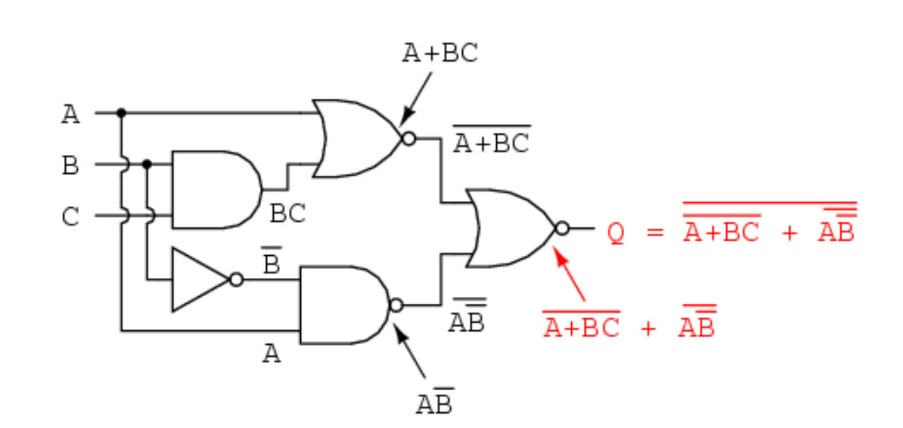
1. Desain Rangkaian Digital
Aljabar Boolean sangat penting dalam desain rangkaian digital. Rangkaian digital adalah susunan saklar dan gerbang logika yang menghasilkan output berdasarkan input yang diberikan.
Aljabar Boolean digunakan untuk menganalisis, merancang, dan mengoptimasi rangkaian ini. Dengan menggunakan ekspresi boolean dan operasi logika AND, OR, NOT, dan lainnya, perancang dapat menghasilkan sirkuit elektronik yang dapat melakukan tugas-tugas kompleks seperti perhitungan, kontrol, dan pengambilan keputusan.
2. Pemrograman Komputer
Aljabar Boolean memiliki peran penting dalam pemrograman komputer. Di dalam bahasa pemrograman, kita menggunakan ekspresi boolean untuk mengontrol alur program, membuat keputusan, dan melakukan perbandingan.
Struktur percabangan seperti “if”, “else”, dan “while” sangat bergantung pada logika boolean untuk mengatur alur program berdasarkan kondisi tertentu.
3. Optimisasi Kueri dalam Basis Data
Dalam basis data, operator logika boolean digunakan untuk mengoptimalkan kueri. Ini memungkinkan kita untuk menggabungkan beberapa kriteria pencarian menggunakan operasi AND, OR, dan NOT.
Misalnya, dalam kueri SQL, Anda dapat menggunakan operator boolean untuk mengambil data berdasarkan kriteria yang kompleks.
4. Sistem Keamanan dan Pengendalian Akses
Aljabar Boolean digunakan dalam implementasi sistem keamanan dan pengendalian akses. Konsep-konsep seperti hak akses pengguna dan grup, perizinan, dan kebijakan akses dapat diwujudkan menggunakan operasi logika boolean.
Ini memungkinkan administrator sistem untuk mengatur siapa yang memiliki akses ke data dan sumber daya tertentu.
5. Rekayasa Perangkat Keras dan Mikrokontroler
Dalam bidang rekayasa elektronika, aljabar Boolean digunakan dalam desain dan analisis sirkuit elektronik, terutama dalam perangkat keras digital dan mikrokontroler.
Ini membantu insinyur merancang dan menguji sirkuit logika yang memiliki fungsi-fungsi spesifik.
6. Pencarian dan Analisis Data dalam Bioinformatika
Aljabar Boolean juga digunakan dalam bioinformatika untuk analisis data genetik dan pencarian dalam basis data genetik. Operator boolean memungkinkan para ilmuwan untuk melakukan pencarian kompleks dan analisis data genetik yang sangat besar dengan efisien.
7. Keamanan Kriptografi
Keamanan kriptografi bergantung pada operasi logika boolean dalam mengenkripsi dan mendekripsi pesan. Algoritma kriptografi menggunakan operasi seperti XOR dan fungsi boolean lainnya untuk melindungi data dan informasi rahasia.
Penutup
Dalam kesimpulannya, aljabar Boolean adalah fondasi matematika yang penting dalam ilmu komputer dan teknik elektronika. Dengan memahami prinsip-prinsip dan hukum-hukumnya, kita dapat mengembangkan solusi yang efisien dan akurat dalam analisis dan perancangan sistem berbasis logika boolean.